Journey to the Center of Infinity

So... are we there yet?

It is way bigger than you think

Think of the biggest number possible. Let me give you some help. A googolplex is the largest named number that is equal to 10 raised to the power of a googol (\(\text{googol} = 10^{100}\)). To put it into perspective, there are around \(10^{80}\) atoms in the known universe.

\[\text{googolplex} = 10^{\text{googol}}\]

Then there is Graham’s number, which was derived by Ronald Graham in the late 1970s. Graham’s number is connected to a problem in Ramsey theory, which is an area in mathematics that deals with combinatorial objects. The problem deals with finding the nodes in an n-dimensional hypercube. Graham’s number is the upper bound of this problem. This number is so extremely large that it can’t even be written exactly.

Graham's Number is given by the upper bound of the following problem: Connect each pair of geometric vertices of an n-dimensional hypercube to obtain a complete graph on 2^n vertices. Color each of the edges of this graph either red or blue. What is the smallest value of n for which every such coloring contains at least one single-colored complete subgraph on four coplanar vertices?.

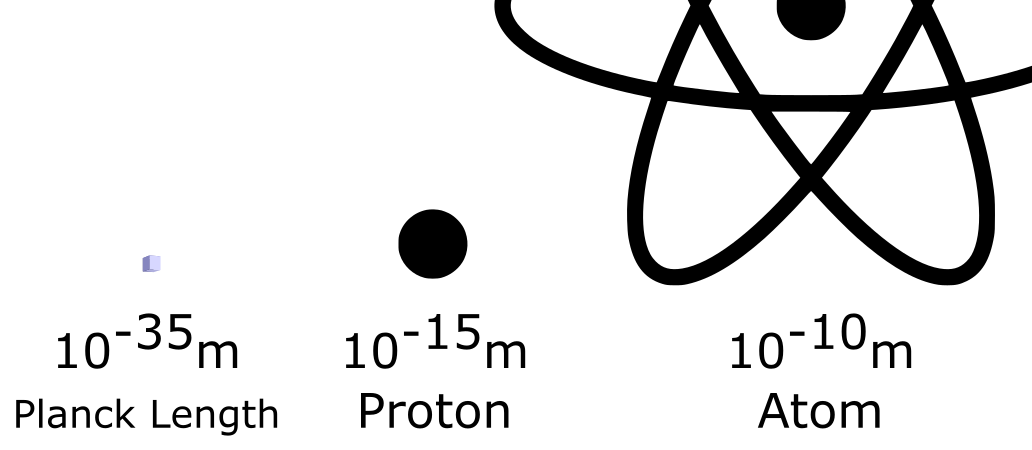
You might think that this doesn’t make much sense, but in the same way that one would instinctively know that an adult has to be taller than a baby, we can also intuitively define that this upper bound is much bigger than any other quantity. So large that there is no physical analogy that I can give you. If we were to pixelate the entire universe in the smallest possible size allowed in quantum physics, that would still only give us a mere \(10^{184}\). Which is only slightly bigger than a googolplex, and minuscule compared to Graham’s number.

Let’s take Graham’s number and see how much bigger we can go. We could simply have Graham’s number to the power of itself, but let’s just use an even more powerful tool. The hyper-operators. The Knuth arrow notation (\(\uparrow\)) might not be a symbol you are used to, but it can represent nested exponentiation concisely.

\[2 \uparrow 4 = 2\times(2\times(2\times 2)) = 2^4 = 16\] \[2 \uparrow\uparrow 4 = 2 \uparrow (2 \uparrow (2 \uparrow 2))= 2^{2^{2^{2}}} = 2^{16} = 65,536\] \[2 \uparrow\uparrow\uparrow 4 = 2 \uparrow\uparrow (2 \uparrow\uparrow (2 \uparrow\uparrow 2 )) = 2 \uparrow\uparrow 65,536\]

Although these hyper-operations can be powered up even further using the Conway chained arrow notation, this should suffice for now. Now let’s try applying this tool to the already ridiculously big Graham’s number. Consider using it as a base for the pentation and itself for the pentation exponent. And just for kicks, let’s just take the factorial The factorial of a number would be a series of operations in a number multiplied by the same number minus one until it is multiplied by 1 $$a! = a \times (a - 1) \times ... \times 1 $$ of this:

\[(G \uparrow \uparrow \uparrow G)! = \text{An impossibly large number}\]

Even after defining an already impossibly large number and using an operator that skyrockets it to a power of itself, this is still microscopic when compared to infinity. Graham’s number goes beyond a number that would be possible in this universe, so it is quite a challenge to comprehend the vastness of infinity. Yet we use infinity constantly in mathematics. Its use dates back to the 4th century BC with Euclid’s fundamental work in geometry and is also the basis for the development of calculus by Newton and Leibniz around 350 years ago. Infinity’s abstract and unmeasurable essence defines many fundamental tools in mathematics, but its purely conceptual nature sparked a loud debate. This became the casus bellian act or situation that provokes or justifies a war for a war that endangered the very nature of mathematics If this section seems interesting to you, you can continue reading about impossibly large numbers in "The Biggest Number in the World: A Journey to the Edge of Mathematics" a book by David Darling and Agnijo Banerjee.

The Intuitionists against the Formalists

What later became known as the “Foundational Crisis of Mathematics” Personally the title is a bit much, was a conflict between formalists and intuitionists that lasted from the late 19th century to the mid-20th century. On one side of the ring, you had the “formalists”, who believed that infinity was just a symbol, a tool used to make calculations easier. And at the other end were the “intuitionists” who believed that infinity was an actual entity, that it existed in a Platonic sense. Several factors sparked this debate, such as the discovery of applications for non-Euclidean geometry and a search for better-defined mathematical limits, but the biggest instigator was the German mathematician Georg Cantor.

Cantor is historically remembered for developing set theory, which is a branch of mathematics that studies collections of objects/numbers. Names such as Real Numbers, Imaginary Numbers, and Natural Numbers might help you remember the topic Unfortunately, this superficially simple theory made Cantor persona non grata among many mathematicians for the consequences that it provoked. While Cantor’s mathematical proof is well-documented and relatively simple, we can neglect much of the mathematics and rely on simple intuition.

Natural numbers are a very simple set. These are always positive, whole numbers, and they do not include any fractions or decimals. Let’s take this set and put it in a box marked with the symbol \(\mathbb{N}\):

\[1\qquad 2\qquad 3\qquad 4\qquad 5\qquad 6\qquad \infty \rightarrow\] \[\downarrow\] \[\begin{CD} . @= . \\ @. @| @|\\ @. . @= . \end{CD}\] \[\qquad \quad \mathbb{N}\]

Natural numbers are a subset of Real numbers, which also include fractions, irrational numbers, and so on. Let’s put this set on a fresh box marked with the symbol \(\mathbb{R}\):

\[\leftarrow -\infty\quad -3\quad -2\quad -1\quad -0.5\qquad 0\qquad 0.5\qquad 1\qquad 2\qquad 3\qquad \infty \rightarrow\] \[\downarrow\] \[\begin{CD} . @= . \\ @. @| @|\\ @. . @= . \end{CD}\] \[\qquad \quad \mathbb{R}\]

Although both boxes contain an infinite amount of numbers, you could instinctively claim that there is more “stuff” in the box that has the real numbers. The set of real numbers includes natural numbers besides other sets, so the infinite number of things in one box must be bigger than the other:

\[\begin{CD} . @= .\\ @| @|\\ . @= .\\@. \vcenter{\hbox{$\displaystyle \mathrm{\mathbb{N}}$}} @. \end{CD} \qquad < \qquad \begin{CD} . @= .\\@| @|\\ . @= .\\@. \vcenter{\hbox{$\displaystyle \mathrm{\mathbb{R}}$}} @.\end{CD}\]

That leads to a strange outcome that breaks any statement in the previous section. You can quantify infinity. It’s no longer an abstract tool like functions, combinatorics, or graphs. This outraged the formalists, who could not fathom considering infinity as anything else. But it was too late. As David Hilbert, a famous German mathematician piously puts it:

“No one shall expel us from the paradise that Cantor has created”

Indeed, the genie was out of the bottle and the nature of mathematics was put into question. What is the proper role of intuition in mathematical reasoning? Is mathematics truly objective or absolute? What is the nature of similar mathematical objects? These are philosophical questions, but these led to the advancement of computer science, model theory, and theoretical physics.

However, there is no satisfying end to this story. Both the intuitionists and formalists developed multiple solutions to the apparent paradox. All of them relied on methods to formalize the rules in mathematics, which were each successful in their regard but did not resolve this crisis independently. Formalism, intuitionism, and the theory of types all played important roles in the development of modern mathematics, and together they helped to establish a more rigorous and consistent foundation for the subject. Thanks to this new consistency, most mathematicians would agree that the paradoxes and contradictions that once plagued the subject are now resolved.

The questions that sparked this debate were not answered. But how could they? When mathematics itself says that they cannot be answered. In 1931, Kurt Gödel showed that any consistent axiomatic system that is powerful enough to encompass arithmetic must be incomplete. Incomplete meaning that there are true mathematical statements that cannot be proved or disproved within the system’s rules. Who would've thought that math was such a rebel A proof that shows mathematical proofs are inherently fallible and that mathematical knowledge will never be fully complete is a paradox that would depress any mathematician if considered. Note that this is a currently accepted fact, but does not imply that this will always be true Perhaps it is enough reason to ignore the statement and focus on something completely different. It is worth noting that this only refers to a subset of the field. Many mathematicians are working towards a complete solution such as Harvey Friedman and Solomon Feferman However, where there are limitations, the search for an answer might lead to other discoveries.

Further analysis of the conflict between the Intuitionists and the Formalists and the infinity problem was done by Veritasium in a video titled "Math's Fundamental Flaw".

Infinity in a physical world

While scientists have recently rejected philosophy towards a tendency for objective truth, the philosophical paradox of infinity can lead to some very interesting ideas. For over two thousand years, Zeno’s paradoxes have challenged our understanding of the physical world. In the fifth century BCE, a Greek philosopher named Zeno of Elea came up with the paradoxes. According to Zeno, the world we see around us is illusory, and only reason can reveal true reality. The purpose of his paradoxes was to illustrate the limitations of human perception and the limitations of our understanding of the physical world. Let’s look at an example of one of the paradoxes:

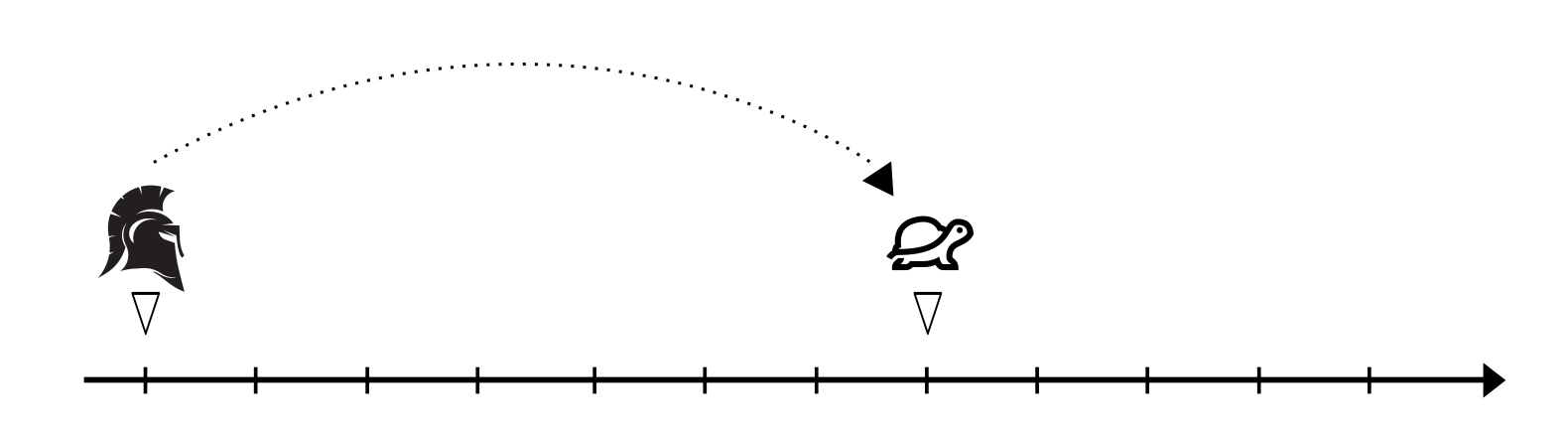
While traveling, Aristotle met the great Greek hero Achilles. Fictional tale Knowing his legendary renown, he knew Achilles wouldn’t back down from a simple challenge. Aristotle challenged Achilles to a footrace against a tortoise, with the rule that Achilles can only move to a position already covered by the tortoise. Considering the ridiculous assumption that he would be beaten by the small animal, Achilles accepted the challenge and gave the tortoise a considerable advantage:

Achilles laughed at the poor pace that the tortoise had, and reached its last position in no time. He would beat the animal without breaking a sweat:

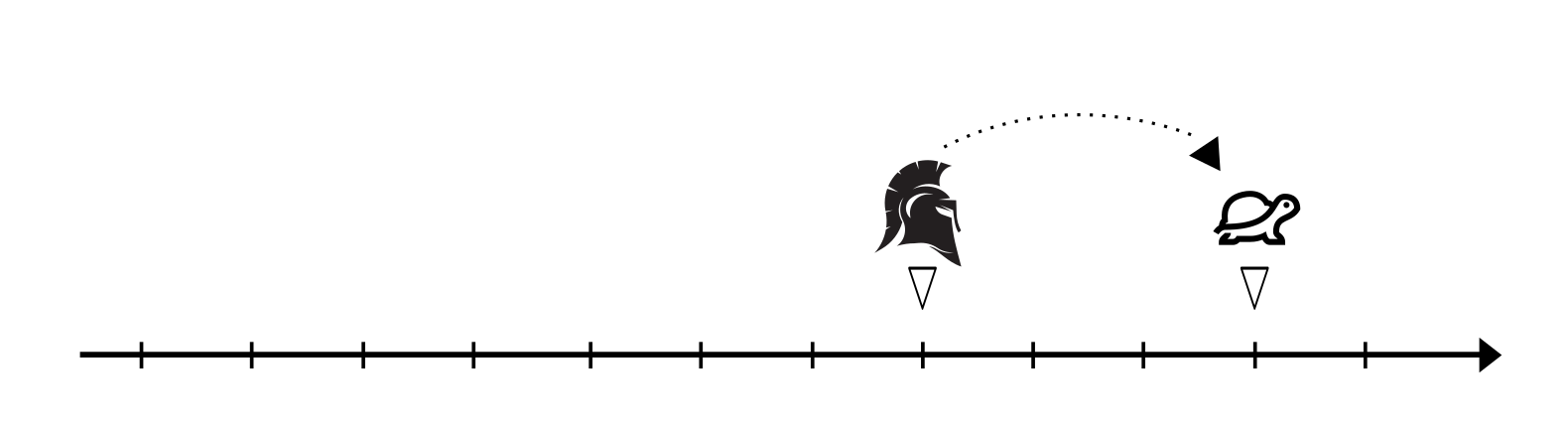
Noticing the apparent frustration of Achilles not being able to overtake the tortoise, Aristotle chimed in with the reminder of the challenge “You can only move to where the tortoise has already been”.

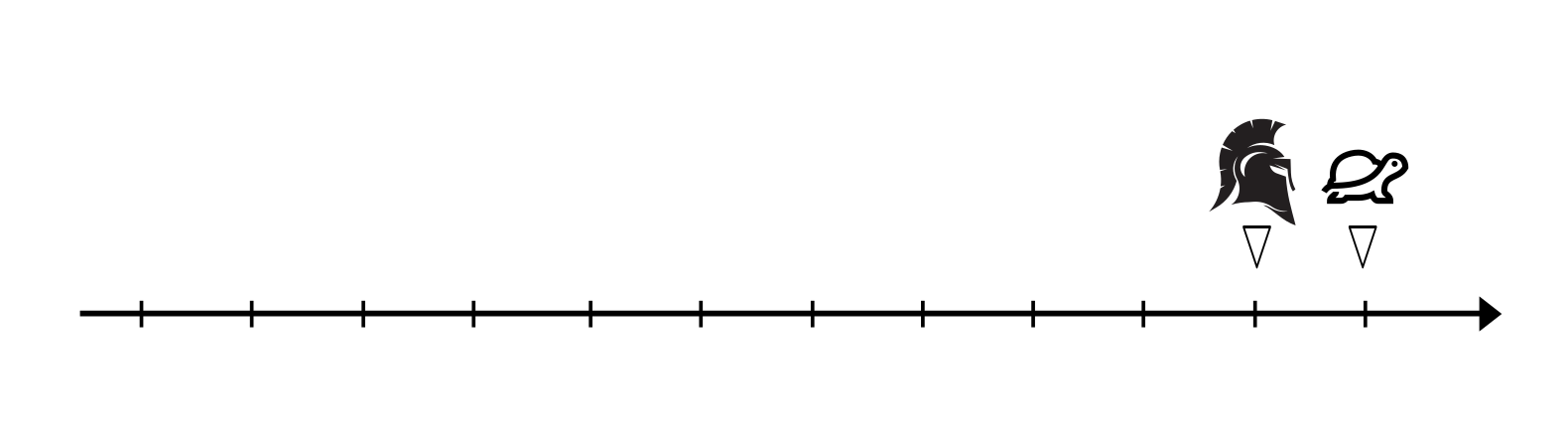
It was too late before Achilles understood the trick. There was no way that he would be able to get ahead of the turtle even if he was twice as fast as he is now. For this, Aristotle stated the obvious fact that was forgotten “In a race, the quickest runner can never over­take the slowest, since the pursuer must first reach the point whence the pursued started so that the slower must always hold a lead”.

While the tale might seem silly at first, it presents a questionable statement about reality. To stick to the rules, could Achilles travel an infinitely decreasing space to reach the tortoise’s last position? As British mathematician Bertrand Russell claimed, the paradox is “immeasurably subtle and profound”. As we now know, the idea of an infinitely smaller space is not allowed in our current understanding of physics. While a deeper explanation would require much more involved reasoning Justifiably its separate article in the future we can limit the smallest size that we can measure to the Planck length$$l_P = \sqrt{\frac{\hbar G}{c^3}}$$ $$l_P = \text{Planck length}$$ $$ \hbar = \text{Reduced Planck constant;}$$ $$ G = \text{Gravitational constant;}$$ $$ c = \text{Speed of light} $$. By introducing the limit of our measurements to a volume of this length we can know how much smaller we are allowed to work with, and this quantity is not infinitely small. Even if we were to replace Achilles and the tortoise with perfectly tuned robots with perfectly tuned measurement devices, our measurements would start to become unmanageable way before reaching the Planck length.

Relative scale of the Planck length. Measurements for the Atom and the proton are their respective radius. Figures for each object are not to scale

What about if we went in the other direction? As far as we know, there is no limit to how big an object can be That is, as long as it doesn't collapse under its weight by the Tolman-Oppenheimer-Volkoff limit. Which again, is a separate topic of discussion. That being said, you might have heard of statements regarding measuring the size of the universe. It is how we can make the previous statement that there are around \(10^{80}\) atoms in the known universe. However, this contrasts with observations of the cosmic microwave background radiation and large-scale structures that appear to be distributed uniformly on scales up to hundreds of millions of light-years. These all point to the fact that as far as we can tell, the universe’s expansiveness is infinite. How are these ideas able to reconcile with each other? We can measure the observable universe, which is estimated to be about 93 billion light-years in diameter, but the universe is considered infinite in terms of its extent. Light takes time to travel these massive distances, and by the time they reach an observer, they’ve already become outdated measurements. In addition, results agree that the universe’s expansion is accelerating, without any sign that it could stop. So even if the size of the universe was not infinity, it appears to be heading in that direction.

Even though they lead to paradoxical statements, both are considered to be true under relativity. It might seem counter-intuitive, but this is stemming from a challenge in scientific understanding. Multiple theories regarding the same phenomena can be correct under their own set of circumstances. Even though it might seem infuriating as a student, this allows a flexible research approach. This leads to novel research, which was the cause, conclusion, and remnants of the foundational crisis of mathematics.

Yeah, we are not quite there yet

The paradox of infinity has challenged and inspired human understanding for thousands of years, from the ancient Greeks to modern scientists. It raises significant questions about the nature of space and time and challenges our understanding of the physical world. The pursuit of knowledge and understanding in mathematics and science has led to substantial developments and advancements. The existence of multiple theories and explanations for a phenomenon is not a weakness, but rather a strength that allows for continued exploration and discovery. As we continue to explore the mysteries of nature, the pursuit of knowledge in mathematics and physics will continue to be intertwined. This is because each field informs and inspires the other. As we think about the paradox of infinity, we are reminded of the beauty and complexity of the universe. We are also reminded of how endless the possibilities of discovery and exploration are. It illustrates the complex and contradictory nature of academia, where differing theories and ideas can contradict and work against each other. While this can be frustrating and challenging, it ultimately leads to a more dynamic and innovative environment for scientific inquiry. The pursuit of knowledge and understanding requires the willingness to challenge established beliefs and explore novel ideas, and this often involves engaging in rigorous debate and criticism. While we may never fully understand the true nature of infinity, the pursuit of knowledge and understanding continues to inspire us to push the limits of our understanding. This leads to discoveries and breakthroughs that benefit all of humanity.

“Science is not only compatible with spirituality; it is a profound source of spirituality. When we recognize our place in an immensity of light years and in the passage of ages, when we grasp the intricacy, beauty, and subtlety of life, then that soaring feeling, that sense of elation and humility combined, is surely spiritual.” - Carl Sagan